B-트리

B - 트리란?

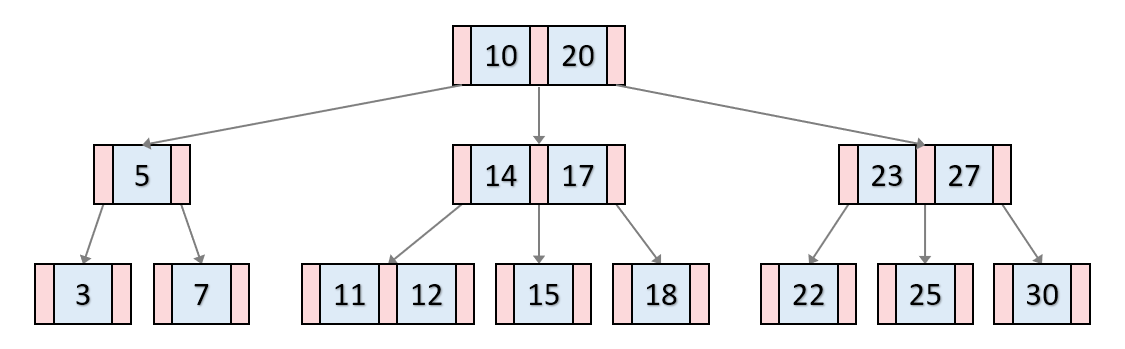
이진트리와는 반대로 자식 노드가 2개 이상인 트리

B - 트리의 조건

1. 모든 단말노드는 동일한 높이
2. 각 내부노드의 자식노드는 M/2 이상, M 이하
3. 루트의 자식 수는 2개 이상
4. 노드의 키가 x개라면 자식의 수는 x+1개
5. 자료는 정렬된 상태로 저장

B-Tree의 장점

• 포인터의 접근 방식이 적어서 속도 이슈가 적음

• B-Tree는 Balanced Tree로 트리내에 모든 데이터가 정렬된 상태를 유지하기 때문에 등호(=)연산 뿐 아니라 부등호(<, >)연산도 가능하다.
• 데이터의 삽입과 삭제, 탐색의 시간복잡도가 O(logN)으로 동일
• B-Tree는 삽입과 삭제 후에도 균형 트리 유지로 균등한 응답 속도를 보장

B-Tree의 단점

• 삽입과 삭제 시 트리의 균형을 유지하기 위해 복잡한 연산을 수행
• 순차탐색시 중위순회를 수행해서 비효율적

 

시간/공간 복잡도

B-트리	최악
탐색	O(logN)
삽입	O(logN)
수정	O(logN)
삭제	O(logN)
공간 복잡도	O(N)

 

탐색연산

이진탐색트리와 동일한 방식으로 수행

루트에서 시작하여, 하향식으로 탐색 대상의 값을 구분 값과 비교하며 자식 포인터를 찾아나가는 과정으로 진행

BtreeSearch(x, k)
 i = 1
 while i ≤ n[x] and k ≥ keyi[x]        // n[x] means number of keys in x node
    do i = i + 1
if i  n[x] and k = keyi[x]
    then return (x, i)
if leaf [x]
    then return NIL
else
    return BtreeSearch(ci[x], k)

 

삽입연산

1. 삽입될 노드가 어느 위치로 삽입될지 찾아 해당 부모 노드에 삽입
2. 부적절한 상태의 노드가 없다면, 삽입 과정을 종료
3. 만약, 어떤 노드가 너무 많은 항목을 가지고 있다면, 이를 두 노드로 분리 이 과정을 반복적으로 트리를 타고 올라가며 진행 만약 루트 노드를 분리하였다면, 새로운 루트 노드를 생성

💡 부적절한 상태의 노드 : 노드에 허용된 자식 노드의 숫자가 허용된 범위 밖인 노드