1차 근삿값 발견용 최적화 알고리즘, 1차 미분계수를 이용해 함수의 최소값을 찾아가는 방법

학습률만큼 계속 이동하면서 학습하기 때문에 적절한 학습률을 지정해줘야 한다.
이때 비용함수을 사용하여 이 값을 최소화하는 방식을 사용한다.
비용 함수(Cost function)
예측 값과 실제 결과 간의 차이를 비용(Cost)라 하며, 이 Cost를 제곱해서 더한 함수로 만든 것을 비용 함수라고 한다.
제곱했기 때문에 이차함수의 형태를 가지게 되므로 이를 최소화하는 매개변수를 찾아가게끔 경사 하강법을 적용한다.

가설함수의 형태를 결정짓는 것은 매개변수(parameter)라 부르는 θ 이고 이 값을 적절하게 조정하여 실제값 y에 가장 근접한 가설함수를 Training set을 이용하여 도출해야 한다.

경사 하강법의 수식

여기서 a의 값은 step size를 의미한다.
Step size
step size는 적절한 크기로 선택해야 한다. 너무 큰 값으로 설정시 이동 거리가 커지게 되어서 빠르게 수렴을 하는 대신, 최솟값으로 수렴되지 못하고 함숫값이 발산할 여지가 생긴다.
너무 작은 경우에는 발산은 하지 않지만, 최솟값을 찾는데 시간이 걸리게 된다.

Local minima 문제(극값 문제)

에러를 최소화시키는 최적의 파라미터를 찾는 문제에 있어서 아래 그림처럼 파라미터 공간에 수많은 지역적인 홀(hole)들이 존재하여 이러한 local minima에 빠질 경우 전역적인 해(global minimum)를 찾기 힘들게 되는 문제를 일컫는다. 추가로 기계 학습의 성능이 잘 안 나오는 이유도 학습 도중 이러한 local minima에 빠졌기 때문이다.

이러한 문제를 해결하기 위해서는 momentum이라는 것을 사용한다.
관성을 사용하는 방법으로 이전의 방향을 기억하여 관성처럼 추가적인 이동을 하며 local minima의 문제를 해결할 수 있다.
이 수식에서 vt는 t번째 time step에서 x의 이동 벡터, γ는 관성계수(momentum term) ≈ 0.9, η은 학습률(Learning rate) 나타낸다.
경사 하강법에 대한 파이썬 코드
import numpy as np
import matplotlib.pyplot as plt
X = np.random.rand(100)
Y = 0.2 * X * 0.5
plt.figure(figsize=(8,6))
plt.scatter(X,Y)
plt.show()
def plot_prediction(pred, y): # 예측값
plt.figure(figsize=(8,6))
plt.scatter(X,y) # 실제값
plt.scatter(X,pred)
plt.show()
## 경사 하강법 구현
W = np.random.uniform(-1,1) 0
b = np.random.uniform(-1,1) # bias
learning_rate = 0.7
for epoch in range(200):
Y_Pred = W * X + b # 예측값
error = np.abs(Y_Pred - Y).mean()
if error < 0.001:
break
# 경사 하강법 계산
w_grad = learning_rate * ((Y_Pred - Y) * X).mean()
b_grad = learning_rate * ((Y_Pred - Y)).mean()
# w, b 값 갱신
W = W - w_grad
b = b - b_grad
if epoch % 10 == 0:
Y_Pred = W * X + b
plot_prediction(Y_Pred, Y) # 예측과 실제 비교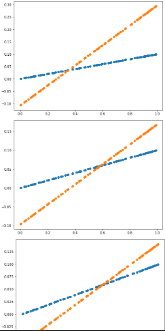
경사 하강법 종류
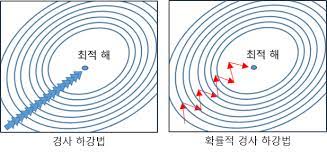
배치 경사 하강법(Batch Gradient Descent)
- 가장 기본적인 경사 하강법이다. 배치 경사 하강법은 데이터셋 전체를 고려하여 손실함수를 계산합니다. 배치 경사 하강법은 한 번의 Epoch에 모든 파라미터 업데이트를 단 한 번만 수행합니다. 즉, Batch의 개수와 Iteration은 1이고 Batch size는 전체 데이터의 개수입니다. 파라미터 업데이트할 때 한 번에 전체 데이터셋을 고려하기 때문에 모델 학습 시 많은 시간과 메모리가 필요하다는 단점이 있다.
확률적 경사 하강법(Stochastic Gradient Descent)
- 확률적 경사 하강법은 배치 경사 하강법이 모델 학습 시 많은 시간과 메모리가 필요하다는 단점을 개선하기 위해 제안된 기법입니다. 확률적 경사 하강법은 Batch size를 1로 설정하여 파라미터를 업데이트하기 때문에 배치 경사 하강법보다 훨씬 빠르고 적은 메모리로 학습이 진행된다.
미니 배치 경사 하강법(Mini-Batch Gradient Descent)
- 미니 배치 경사 하강법(Mini-Batch Gradient Descent)은 Batch size가 1도 전체 데이터 개수도 아닌 경우를 말합니다. 미니 배치 경사 하강법은 배치 경사 하강법보다 모델 학습 속도가 빠르고, 확률적 경사 하강법보다 안정적인 장점이 있습니다. 그 이유로 딥러닝 분야에서 가장 많이 활용하는 경사 하강법입니다. 추가로 Batch size는 일반적으로 32, 64, 128과 같이 2ⁿ에 해당하는 값으로 사용하는 게 보편적이다.
용어?
epoch: 학습 횟수
- Ex.) epoch가 10이면 10번 반복
Batch size : 모델의 가중치를 한번 업데이트시킬 때 사용되는 샘플들의 묶음
- Ex.) 1000개의 훈련 샘플중 배치 사이즈가 20이라면 20개의 샘플 단위마다 모델의 가중치를 한번에 업데이트
Iteration : epoch을 나누어서 실행하는 횟수, 반복 횟수
- Ex.) 총 데이터가 2000개, batch size = 500, epochs = 20일 때
- 1 Epoch = 총 데이터(2000)/ batch size(500) = 4 iteration(4번 반복)
- 전체 데이터셋에 대해서는 20번 학습, iteration 기준으로는 80번의 학습
출처:
https://ko.wikipedia.org/wiki/%EA%B2%BD%EC%82%AC_%ED%95%98%EA%B0%95%EB%B2%95
https://angeloyeo.github.io/2020/08/16/gradient_descent.html
'데이터분석 > ML 이론' 카테고리의 다른 글
| 과대적합, 과소적합 및 해결방법 (0) | 2023.01.09 |
|---|