Prim 알고리즘이란?
시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장해나가는 방법
Prim 알고리즘의 동작 방법
- 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
- 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다. (즉, 가장 낮은 가중치를 먼저 선택한다.)
- 위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복한다.

Prim 알고리즘을 이용한 MST(최소 신장 트리)를 만드는 과정
- 정점 선택을 기반으로 하는 알고리즘
- 이전 단계에서 만들어진 신장 트리를 확장하는 방법
Prim 알고리즘의 시간 복잡도
- for 반복문이 정점의 수 n만큼 반복하고, 내부 반복은 n번 반복(Prim의 경우 O(n²), Kruskal의 경우 O(nlogn))
- 그래프 내에 적은 숫자의 간선만을 가지는 최소 그래프(Sparse Graph)의 경우 Kruskal이 적합
- 그래프에 간선이 많이 존재하는 밀집 그래프(Dense Graph)의 경우는 Prim이 적합
Kruskal 알고리즘이란?
Kruskal 알고리즘이란 탐욕적인 방법(greedy method)을 이용하여 네트워크(가중치를 간선에 할당한 그래프)의 모든 정점을 최소 비용으로 연결하는 최적해답을 구하는 것
- 탐욕적인 방법
- 결정을 해야 할 때마다 그 순간에 가장 좋다고 생각되는 것을 선택함으로써 최종적인 해답에 도달
- 탐욕적인 방법은 그 순간에는 최적이지만, 전체적인 관점에서 최적이라는 보장이 없기 때문에 반드시 검증
- 다행히 Kruskal 알고리즘은 최적의 해답을 주는 것으로 증명
- MST(최소 비용 신장 트리)가
1. 최소 비용의 간선으로 구성 됨
2. 사이클을 포함하지 않음
두 조건에 근거하여 각 단계에서 사이클을 이루지 않는 최소 비용 간선을 선택
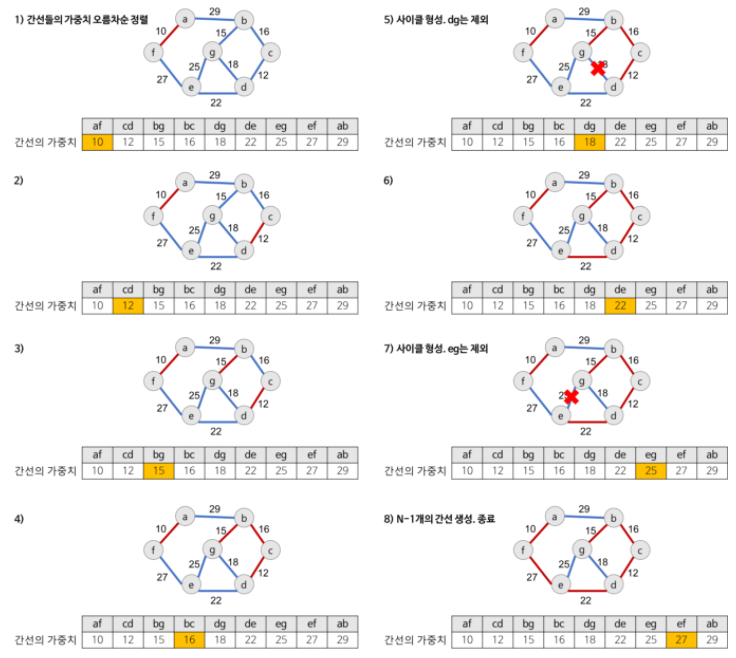
Kruskal 알고리즘의 동작 방법
간선 선택을 기반으로 하는 알고리즘 이전 단계에서 만들어진 신장 트리와는 상관없이 무조건 최소 간선만을 선택하는 방법
※ 주의사항
- 다음 간선을 이미 선택된 간선들의 집합에 추가할 때 사이클을 생성하는지를 체크!
- 새로운 간선이 이미 다른 경로에 의해 연결되어 있는 정점들을 연결할 때 사이클이 형성된다. 즉, 추가할 새로운 간선의 양끝 정점이 같은 집합에 속해 있으면 사이클이 형성된다.
- 사이클 생성 여부를 확인하는 방법 추가하고자 하는 간선의 양끝 정점이 같은 집합에 속해 있는지를 먼저 검사해야 한다.
Kruskal 알고리즘의 결과가 최선임을 증명
해당 식은 가중치 그래프 G의 최소 신장 트리 T(e<E1에 대해 가중치 w(e)>= 0는 양을 최소화하는 신장 트리이다.

Kruskal 알고리즘을 최소 신장 트리 찾는 알고리즘이고 Kruskal 알고리즘은 연결된 그래프의 최소 신장 트리를 생성한다. 알고리즘의 단계 t에서 생성된 Forest(Ft)를 호출한다. 그런 다음 F0는 G의 모든 정점 집합이고 F{n-1}은 Kruskal 알고리즘, 숲의 최종 결과물이다.
추가적으로 n 정점의 모든 최소 신장 트리가 n-1의 가장자리를 가지고 있음을 증명하므로 n-1 단계 이후에 중지한다. 알고리즘이 Fi에 주기가 없음을 보장하기 때문에 F{n-1}이 트리임이 증명한다.
그리고 n-1개의 모서리를 가진 모든 트리는 반드시 신장 트리여야 한다.
→ 왜냐하면 일부 정점이 누락된 경우 n-1개의 정점으로 구성된 서브 그래프에 n-1개의 모서리가 있기 때문에 필연적으로 해당 서브 그래프에 주기가 발생하기 때문이다.
이제 우리는 F{n-1}이 최소 비용을 갖는다는 것을 증명할 것이다.
실제로 비용이 F{n-1}보다 훨씬 낮은 트리 T가 있다고 가정하면 (T가 최소라고 가정할 수도 있지만 필수적은 아니다). $F_{n-1}$에 없는 최소 가중치 간선 e를 선택하고 F{n-1}에 e를 추가하면 F{n-1}에 고유한 주기 C가 도입된다. 하지만 주기에는 몇 가지 이상한 점이 있다.
첫째, e는 C의 모든 간선 중 비용이 가장 높다.
그렇지 않은 경우 Kruskal의 알고리즘은 더 무거운 가중치 가장자리보다 먼저 선택했을 것이다.
둘째, T에 없는 또 다른 간선이 C에 있습니다(T는 트리이기 때문에 전체 주기를 가질 수 없습니다).
그런 모서리를 e in T라고 부릅니다. 이제 F{n-1}에서 e'를 제거하고 e를 추가할 수 있다. 이것은 F{n-1}의 총 비용만 증가 시킬 수 있다. 그러나, 이 변환은 이전보다 T와 공통된 모서리가 하나 더 있는 트리를 생성한다. 이것은 T가 F{n-1}보다 엄격하게 낮은 가중치를 가지고 있다는 것과 모순된다. 우리가 설명한 프로세스를 반복하면 결국 총 비용만 증가하면서 F{n-1}을 T로 정확히 변환할 것이기 때문이다.
따라서 이 경우에는 알고리즘은 최소 신장 트리를 찾는 데 최적으로 수행된다.
'알고리즘 공부 > Greedy Algorithm' 카테고리의 다른 글
| 탐욕알고리즘의 예시 (0) | 2022.01.03 |
|---|---|
| 매트로이드 이론 (0) | 2022.01.01 |
| 탐욕 알고리즘 - 개요 (3) | 2022.01.01 |